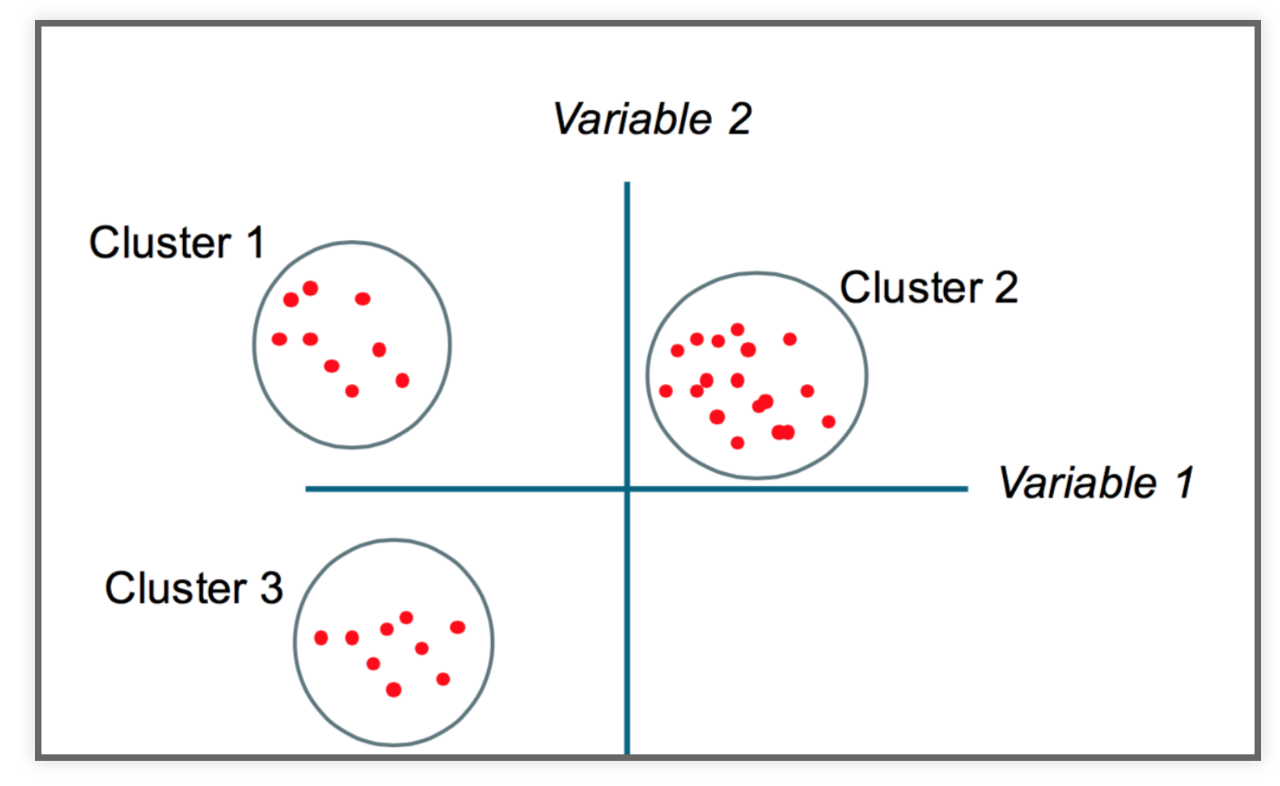
Some intuition¶
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import geopandas as gpd
np.random.seed(42)
%matplotlib inline
plt.rcParams['figure.figsize'] = (10,6)
Nov 5, 2020
The goal
Partition a dataset into groups that have a similar set of attributes, or features, within the group and a dissimilar set of features between groups.
Minimize the intra-cluster variance and maximize the inter-cluster variance of features.

import altair as alt
from vega_datasets import data as vega_data
Read the data from a URL:
gapminder = pd.read_csv(vega_data.gapminder_health_income.url)
gapminder.head()
| country | income | health | population | |
|---|---|---|---|---|
| 0 | Afghanistan | 1925 | 57.63 | 32526562 |
| 1 | Albania | 10620 | 76.00 | 2896679 |
| 2 | Algeria | 13434 | 76.50 | 39666519 |
| 3 | Andorra | 46577 | 84.10 | 70473 |
| 4 | Angola | 7615 | 61.00 | 25021974 |
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5)
StandardScaler classfrom sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
Use the fit_transform() function to scale your features
gapminder_scaled = scaler.fit_transform(gapminder[['income', 'health', 'population']])
Now fit the scaled features
# Perform the fit
kmeans.fit(gapminder_scaled)
# Extract the labels
gapminder['label'] = kmeans.labels_
alt.Chart(gapminder).mark_circle().encode(
alt.X('income:Q', scale=alt.Scale(type='log')),
alt.Y('health:Q', scale=alt.Scale(zero=False)),
size='population:Q',
color=alt.Color('label:N', scale=alt.Scale(scheme='dark2')),
tooltip=list(gapminder.columns)
).interactive()
I've extracted neighborhood Airbnb statistics for Philadelphia neighborhoods from Tom Slee's website.
The data includes average price per person, overall satisfaction, and number of listings.
Original research study: How Airbnb's Data Hid the Facts in New York City
The data is available in CSV format ("philly_airbnb_by_neighborhoods.csv") in the "data/" folder of the repository.
airbnb = pd.read_csv("data/philly_airbnb_by_neighborhoods.csv")
airbnb.head()
| neighborhood | price_per_person | overall_satisfaction | N | |
|---|---|---|---|---|
| 0 | ALLEGHENY_WEST | 120.791667 | 4.666667 | 23 |
| 1 | BELLA_VISTA | 87.407920 | 3.158333 | 204 |
| 2 | BELMONT | 69.425000 | 3.250000 | 11 |
| 3 | BREWERYTOWN | 71.788188 | 1.943182 | 142 |
| 4 | BUSTLETON | 55.833333 | 1.250000 | 19 |
price_per_person, overall_satisfaction, N# Initialize the Kmeans object
kmeans = KMeans(n_clusters=5, random_state=42)
# Scale the data features we want
scaler = StandardScaler()
scaled_data = scaler.fit_transform(airbnb[['price_per_person', 'overall_satisfaction', 'N']])
# Run the fit!
kmeans.fit(scaled_data)
# Save the cluster labels
airbnb['label'] = kmeans.labels_
# New column "label"!
airbnb.head()
| neighborhood | price_per_person | overall_satisfaction | N | label | |
|---|---|---|---|---|---|
| 0 | ALLEGHENY_WEST | 120.791667 | 4.666667 | 23 | 1 |
| 1 | BELLA_VISTA | 87.407920 | 3.158333 | 204 | 1 |
| 2 | BELMONT | 69.425000 | 3.250000 | 11 | 1 |
| 3 | BREWERYTOWN | 71.788188 | 1.943182 | 142 | 1 |
| 4 | BUSTLETON | 55.833333 | 1.250000 | 19 | 0 |
To gain some insight into our clusters, after calculating the K-Means labels:
label columnmean() of each of our featuresairbnb.groupby('label', as_index=False).size()
| label | size | |
|---|---|---|
| 0 | 0 | 19 |
| 1 | 1 | 69 |
| 2 | 2 | 1 |
| 3 | 3 | 1 |
| 4 | 4 | 15 |
airbnb.groupby('label', as_index=False).mean().sort_values(by='price_per_person')
| label | price_per_person | overall_satisfaction | N | |
|---|---|---|---|---|
| 1 | 1 | 73.199020 | 3.137213 | 76.550725 |
| 0 | 0 | 79.250011 | 0.697461 | 23.473684 |
| 4 | 4 | 116.601261 | 2.936508 | 389.933333 |
| 2 | 2 | 136.263996 | 3.000924 | 1499.000000 |
| 3 | 3 | 387.626984 | 5.000000 | 31.000000 |
airbnb.loc[airbnb['label'] == 2]
| neighborhood | price_per_person | overall_satisfaction | N | label | |
|---|---|---|---|---|---|
| 75 | RITTENHOUSE | 136.263996 | 3.000924 | 1499 | 2 |
airbnb.loc[airbnb['label'] == 3]
| neighborhood | price_per_person | overall_satisfaction | N | label | |
|---|---|---|---|---|---|
| 78 | SHARSWOOD | 387.626984 | 5.0 | 31 | 3 |
airbnb.loc[airbnb['label'] == 4]
| neighborhood | price_per_person | overall_satisfaction | N | label | |
|---|---|---|---|---|---|
| 16 | EAST_PARK | 193.388889 | 2.714286 | 42 | 4 |
| 19 | FAIRMOUNT | 144.764110 | 2.903614 | 463 | 4 |
| 20 | FISHTOWN | 59.283468 | 2.963816 | 477 | 4 |
| 23 | FRANCISVILLE | 124.795795 | 3.164062 | 300 | 4 |
| 35 | GRADUATE_HOSPITAL | 106.420417 | 3.180791 | 649 | 4 |
| 47 | LOGAN_SQUARE | 145.439414 | 3.139241 | 510 | 4 |
| 57 | NORTHERN_LIBERTIES | 145.004866 | 3.095506 | 367 | 4 |
| 60 | OLD_CITY | 111.708084 | 2.756637 | 352 | 4 |
| 70 | POINT_BREEZE | 63.801072 | 2.759542 | 435 | 4 |
| 72 | QUEEN_VILLAGE | 106.405744 | 3.125000 | 248 | 4 |
| 79 | SOCIETY_HILL | 133.598667 | 3.118421 | 165 | 4 |
| 82 | SPRING_GARDEN | 157.125692 | 3.454023 | 413 | 4 |
| 83 | SPRUCE_HILL | 48.095512 | 2.377358 | 399 | 4 |
| 88 | UNIVERSITY_CITY | 82.228062 | 2.231579 | 326 | 4 |
| 91 | WASHINGTON_SQUARE | 126.959118 | 3.063745 | 703 | 4 |
./data/philly_neighborhoods.geojsoncategorical=True and legend=True keywords will be useful herehoods = gpd.read_file("./data/philly_neighborhoods.geojson")
hoods.head()
| Name | geometry | |
|---|---|---|
| 0 | LAWNDALE | POLYGON ((-75.08616 40.05013, -75.08893 40.044... |
| 1 | ASTON_WOODBRIDGE | POLYGON ((-75.00860 40.05369, -75.00861 40.053... |
| 2 | CARROLL_PARK | POLYGON ((-75.22673 39.97720, -75.22022 39.974... |
| 3 | CHESTNUT_HILL | POLYGON ((-75.21278 40.08637, -75.21272 40.086... |
| 4 | BURNHOLME | POLYGON ((-75.08768 40.06861, -75.08758 40.068... |
airbnb.head()
| neighborhood | price_per_person | overall_satisfaction | N | label | |
|---|---|---|---|---|---|
| 0 | ALLEGHENY_WEST | 120.791667 | 4.666667 | 23 | 1 |
| 1 | BELLA_VISTA | 87.407920 | 3.158333 | 204 | 1 |
| 2 | BELMONT | 69.425000 | 3.250000 | 11 | 1 |
| 3 | BREWERYTOWN | 71.788188 | 1.943182 | 142 | 1 |
| 4 | BUSTLETON | 55.833333 | 1.250000 | 19 | 0 |
# do the merge
airbnb2 = hoods.merge(airbnb, left_on='Name', right_on='neighborhood', how='left')
# assign -1 to the neighborhoods without any listings
airbnb2['label'] = airbnb2['label'].fillna(-1)
# plot the data
airbnb2 = airbnb2.to_crs(epsg=3857)
# setup the figure
f, ax = plt.subplots(figsize=(10, 8))
# plot, coloring by label column
# specify categorical data and add legend
airbnb2.plot(
column="label",
cmap="Dark2",
categorical=True,
legend=True,
edgecolor="k",
lw=0.5,
ax=ax,
)
ax.set_axis_off()
plt.axis("equal");
Use altair to plot the clustering results with a tooltip for neighborhood name and tooltip.
Hint: See week 3B's lecture on interactive choropleth's with altair
# plot map, where variables ares nested within `properties`,
alt.Chart(airbnb2.to_crs(epsg=4326)).mark_geoshape().properties(
width=500, height=400,
).encode(
tooltip=["Name:N", "label:N"],
color=alt.Color("label:N", scale=alt.Scale(scheme="Dark2")),
)
Cluster #3 seems like the best bang for your buck!
Now on to the more traditional view of "clustering"...
"Density-Based Spatial Clustering of Applications with Noise"

min_samples = 4. min_samples (4) points (including the point itself) within a distance of eps from each of these points.eps) from the core points so they are part of the cluster min_pts within a distance of eps so they are not core pointseps from any of the cluster pointsHigher min_samples or a lower eps requires a higher density necessary to form a cluster.
x and y in units of meterscoords = gpd.read_file('./data/osm_gps_philadelphia.geojson')
coords.head()
| x | y | geometry | |
|---|---|---|---|
| 0 | -8370750.5 | 4865303.0 | POINT (-8370750.500 4865303.000) |
| 1 | -8368298.0 | 4859096.5 | POINT (-8368298.000 4859096.500) |
| 2 | -8365991.0 | 4860380.0 | POINT (-8365991.000 4860380.000) |
| 3 | -8372306.5 | 4868231.0 | POINT (-8372306.500 4868231.000) |
| 4 | -8376768.5 | 4864341.0 | POINT (-8376768.500 4864341.000) |
num_points = len(coords)
print(f"Total number of points = {num_points}")
Total number of points = 52358
from sklearn.cluster import dbscan
dbscan?
# some parameters to start with
eps = 50 # in meters
min_samples = 50
cores, labels = dbscan(coords[["x", "y"]], eps=eps, min_samples=min_samples)
The function returns two objects, which we call cores and labels. cores contains the indices of each point which is classified as a core.
# The first 5 elements
cores[:5]
array([ 1, 4, 6, 10, 12])
The length of cores tells you how many core samples we have:
num_cores = len(cores)
print(f"Number of core samples = {num_cores}")
Number of core samples = 19370
The labels tells you the cluster number each point belongs to. Those points classified as noise receive a cluster number of -1:
# The first 5 elements
labels[:5]
array([-1, 0, -1, -1, 1])
The labels array is the same length as our input data, so we can add it as a column in our original data frame
# Add our labels to the original data
coords['label'] = labels
coords.head()
| x | y | geometry | label | |
|---|---|---|---|---|
| 0 | -8370750.5 | 4865303.0 | POINT (-8370750.500 4865303.000) | -1 |
| 1 | -8368298.0 | 4859096.5 | POINT (-8368298.000 4859096.500) | 0 |
| 2 | -8365991.0 | 4860380.0 | POINT (-8365991.000 4860380.000) | -1 |
| 3 | -8372306.5 | 4868231.0 | POINT (-8372306.500 4868231.000) | -1 |
| 4 | -8376768.5 | 4864341.0 | POINT (-8376768.500 4864341.000) | 1 |
The number of clusters is the number of unique labels minus one (because noise has a label of -1)
num_clusters = coords['label'].nunique() - 1
print(f"number of clusters = {num_clusters}")
number of clusters = 87
We can group by the label column to get the size of each cluster:
cluster_sizes = coords.groupby('label', as_index=False).size()
cluster_sizes
| label | size | |
|---|---|---|
| 0 | -1 | 29054 |
| 1 | 0 | 113 |
| 2 | 1 | 4073 |
| 3 | 2 | 1787 |
| 4 | 3 | 3370 |
| ... | ... | ... |
| 83 | 82 | 54 |
| 84 | 83 | 56 |
| 85 | 84 | 50 |
| 86 | 85 | 53 |
| 87 | 86 | 50 |
88 rows × 2 columns
# All points get assigned a cluster label (-1 reserved for noise)
cluster_sizes['size'].sum() == num_points
True
The number of noise points is the size of the cluster with label "-1":
num_noise = cluster_sizes.iloc[0]['size']
print(f"number of noise points = {num_noise}")
number of noise points = 29054
If points aren't noise or core samples, they must be edges:
num_edges = num_points - num_cores - num_noise
print(f"Number of edge points = {num_edges}")
Number of edge points = 3934
x and mean y value for each cluster# Setup figure and axis
f, ax = plt.subplots(figsize=(10, 10), facecolor="black")
# Plot the noise samples in grey
noise = coords.loc[coords["label"] == -1]
ax.scatter(noise["x"], noise["y"], c="grey", s=5, linewidth=0)
# Loop over each cluster number
for label_num in range(0, num_clusters):
# Extract the samples with this label number
this_cluster = coords.loc[coords["label"] == label_num]
# Calculate the mean (x,y) point for this cluster in red
x_mean = this_cluster["x"].mean()
y_mean = this_cluster["y"].mean()
# Plot this centroid point in red
ax.scatter(x_mean, y_mean, linewidth=0, color="red")
# Format
ax.set_axis_off()
ax.set_aspect("equal")
DBSCAN can perform high-density clusters from more than just spatial coordinates, as long as they are properly normalized
I've extracted data for taxi pickups or drop offs occurring in the Williamsburg neighborhood of NYC from the NYC taxi open data.
Includes data for:
Goal: identify clusters of similar taxi rides that are not only clustered spatially, but also clustered for features like hour of day and trip distance
Inspired by this CARTO blog post